C++/Go算法学习 | Linchang Xiao

C++ 基础

class 中的变量权限

类的一个特征就是封装，public 和 private 作用就是实现这一目的。类的另一个特征就是继承，protected 的作用就是实现这一目的
- public：用户代码（类外）可以访问 public 成员而不能访问 private 成员
- protected：protected 成员可以被派生类对象访问，不能被用户代码（类外）访问
- private：private 成员只能由类成员（类内）和友元访问。

inline

C++ 中的函数调用

当程序执行函数调用指令时，CPU 将存储该函数调用后指令的内存地址，将函数的参数复制到堆栈上，最后将控制权转移到指定的函数。然后，CPU 执行函数代码，将函数返回值存储在预定义的内存位置/寄存器中，并将控制权返回给调用函数。
时间消耗分析
- 调用者函数到被调用者的切换时间
- 函数执行时间

CMake

CMake 通常的 build 和编译位置

参考文献：https://blog.csdn.net/shaoyou223/article/details/84764633

mkdir build
cd build
cmake ..
make

# FetchContent 模块用于获取外部依赖库, 在构建生成文件的过程中被调用
include(FetchContent)
# FetchContent_Declare 描述如何下载依赖库
FetchContent_Declare(
    pybind11
    GIT_REPOSITORY https://github.com/pybind/pybind11.git
    GIT_TAG        v2.6.2
    GIT_SHALLOW    TRUE
)
# FetchContent_MakeAvaliable 下载依赖库, 并使其可用
FetchContent_MakeAvailable(pybind11)

CMake 的多版本共存

请不要直接删除 cmake，可能会导致一些文件被删除
多版本共存 CMake 参考文献：https://zhuanlan.zhihu.com/p/442561052

Makefile

Pybind

快速实现 C/C++ 和 Python 的互通参考文献：https://www.jianshu.com/p/0b4b49dd706a
比较复杂的教程，可以实现使用 python 调用 C++ 写的有关 numpy 的算子【来自论文 ELSED: Enhanced Line SEgment Drawing】：https://www.guyuehome.com/38198

C++ 虚函数表

参考文献：https://www.cnblogs.com/Mered1th/p/10924545.html
单继承
- 虚表中派生类覆盖的虚函数的地址被放在了基类相应的函数原来的位置
- 派生类没有覆盖的虚函数就延用基类的。同时，虚函数按照其声明顺序放于表中，父类的虚函数在子类的虚函数前面。
多继承
- 每个基类都有自己的虚函数表
- 派生类的虚函数地址存依照声明顺序放在第一个基类的虚表最后

字符串

字符串截取下标段

string month = time_s.substr(0, 2);
string day = time_s.substr(3, 5);

stoi 和 to_string

int month_n = stoi(month);
int day_n = stoi(day);

string month = to_string(month_n);

数组相关问题

一维数组的排序

int time_arr[4] = {arriveAlice_n, leaveAlice_n, arriveBob_n, leaveBob_n};
sort(time_arr, time_arr+4);

前缀和刷题框架

一维前缀和

class NumArray {
    // 前缀和数组
    private int[] preSum;

    /* 输入一个数组，构造前缀和 */
    public NumArray(int[] nums) {
        // preSum[0] = 0，便于计算累加和
        // 这里是多增加了一个item, 主要是避免条件判断
        preSum = new int[nums.length + 1];
        // 计算 nums 的累加和
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    /* 查询闭区间 [left, right] 的累加和 */
    // 这个函数调用次数很多, 应该尽量避免条件判断和遍历
    public int sumRange(int left, int right) { 
        return preSum[right + 1] - preSum[left];
    }
}

二维前缀和

class NumMatrix {
public:
    NumMatrix(vector<vector<int>>& matrix) {
        vector<int> new_vec = {};
        this->presum.push_back(new_vec);
        for (int j = 0; j <= matrix[0].size(); ++j) {
            this->presum[0].push_back(0);
        }
        
        
        for (int i = 1; i <= matrix.size(); ++i) {
            vector<int> new_vec = {};
            this->presum.push_back(new_vec);
            this->presum[i].push_back(0);
            for (int j = 1; j <= matrix[0].size(); ++j) {
                // 很重要的计算方式
                this->presum[i].push_back(
                    this->presum[i-1][j] - this->presum[i-1][j-1] + this->presum[i][j-1] + matrix[i-1][j-1]
                );
                // cout << "presum[" << i << "][" << j << "]: " << this->presum[i][j] << endl;
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        // cout << "this->presum[row2+1][col2+1]: " << this->presum[row2+1][col2+1] << "; this->presum[row2+1][col1+1]: " << this->presum[row2+1][col1+1]
        //     << "; this->presum[row1+1][col2+1]: " << this->presum[row1+1][col2+1] << "; this->presum[row1+1][col1+1]: " << this->presum[row1+1][col1+1] << endl; 
        // 很重要的计算方式
        return this->presum[row2+1][col2+1] - this->presum[row2+1][col1] - this->presum[row1][col2+1] + this->presum[row1][col1];
    }
private:
    vector<vector<int>> presum;
};

前缀和-vector 实现（1）

这是一个常见的算法，可以在只遍历一次的情况下，计算多个区间的统计信息。
方案
- 设置一个前缀和数组 arr，位置 i+1 存储的是第 0 个元素到第 i 个元素的求和（或者其他统计信息）
- 最后计算方案：arr[r+1] - arr[l]
Leetcode 2559

class Solution {
public:
    bool isYuan(string& word) {
        bool result = true;
        int last_index = word.size() - 1;
        if (word[0] != 'a' && word[0] != 'e' && word[0] != 'i' && word[0] != 'o' && word[0] != 'u') {
            result = false;
        }
        if (result && (word[last_index] != 'a' && word[last_index] != 'e' && word[last_index] != 'i' && word[last_index] != 'o' && word[last_index] != 'u')) {
            result = false;
        }
        return result;
    }
    vector<int> vowelStrings(vector<string>& words, vector<vector<int>>& queries) {
        vector<int> num_v = {0};
        int len_num_v = 1;
        for (string& word: words) {
            if (this->isYuan(word)) {
                num_v.push_back(num_v[len_num_v-1] + 1);
            } else {
                num_v.push_back(num_v[len_num_v-1]);
            }
            len_num_v += 1;
        }
        vector<int> result = {};
        for (vector<int>& pair: queries) {
            result.push_back(num_v[pair[1]+1] - num_v[pair[0]]);
        }
        return result;
    }
};

前缀和-stack 实现（2）

leetcode：https://leetcode.cn/problems/remove-zero-sum-consecutive-nodes-from-linked-list/submissions/
方案：用 stack 可以实现一个在线维护更新的前缀和，可以通过 pop 操作将中间的一些情况给删除掉

#include <bits/stdc++.h>
using namespace std;

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
public:

    void print_list(ListNode* result) {
        while (result != NULL) {
            cout << result->val << " ";
            result = result->next;
        }
        cout << endl;
    }
    ListNode* removeZeroSumSublists(ListNode* head) {
        ListNode* current_h = head;
        ListNode* head_extend = new ListNode(-999999, head);

        stack<int> sum_front;
        sum_front.push(0);
        unordered_map<int, ListNode*> sum_2_node;
        while (current_h != NULL) {
            cout << "in current_h: " << current_h->val << endl;
            int old_sum_front = sum_front.top();
            int current_sum_front = old_sum_front + current_h->val;
            ListNode* same_sum_front_node = sum_2_node[current_sum_front];
            if (current_h->val == 0) {
                if (same_sum_front_node != NULL) {
                    same_sum_front_node->next = current_h->next;
                } else {
                    head_extend->next = current_h->next;
                }
            } else {
                cout << "current_sum_front: " << current_sum_front << endl;
                
                if (current_sum_front == 0) { // 全部删除
                    head_extend->next = current_h->next;
                    while (sum_front.size() > 1) {
                        int sum_f = sum_front.top();
                        sum_2_node[sum_f] = NULL;
                        sum_front.pop();
                    }
                } else if (same_sum_front_node != NULL) { // 已经存在
                    same_sum_front_node->next = current_h->next;
                    int sum_f = sum_front.top();
                    while (sum_f != current_sum_front) {
                        sum_2_node[sum_f] = NULL;
                        sum_front.pop();
                        sum_f = sum_front.top();
                    }
                } else {
                    cout << current_sum_front << " push to sum_front" << endl;
                    sum_front.push(current_sum_front);
                    sum_2_node[current_sum_front] = current_h;
                }
            }
            ListNode* print_head_extend = head_extend;
            this->print_list(print_head_extend);

            current_h = current_h->next;
            cout << endl << endl;
        }
 
        return head_extend->next;
        
    }
};

int main() {
    ListNode* node = new ListNode(0);
    node->next = new ListNode(1);
    node->next->next = new ListNode(2);
    node->next->next->next = new ListNode(3);
    node->next->next->next->next = new ListNode(-2);
    node->next->next->next->next->next = new ListNode(-3);
    node->next->next->next->next->next->next = new ListNode(4);
    node->next->next->next->next->next->next->next = new ListNode(-3);
    node->next->next->next->next->next->next->next->next = new ListNode(-2);
    node->next->next->next->next->next->next->next->next->next = new ListNode(0);
    
    Solution* sol = new Solution();
    ListNode* result = sol->removeZeroSumSublists(node);
    
    while (result != NULL) {
        cout << result->val << " ";
        result = result->next;
    }
    cout << endl;
}

vector

二维 vector 排序算法

vector<vector<int>> points;
sort(points.begin(), ppints.end(), [](const vector<int> &a, const vector<int> &b) {
    return a[0] < b[0];
});

快速创建二维 vector 并初始化为 0

vector<vector<int>> res(row, vector<int>(col));

交换 i 和 j 的未知

std::swap(v[i], v[j]);

哈希表

哈希表迭代器

#include <bits/stdc++.h>
using namespace std;

vector<int> res(n);
unordered_map<int, int>::iterator select_it = select_map.begin();
while(select_it != select_map.end()) {
    // cout << "pair select_it.key = " << select_it->first << " pair select_it.value = " << select_it->second << endl;
    res[select_it->first] = select_it->second + 1;
    ++select_it;
}
return res;

// for函数内进行迭代
for (auto iter = this->hashTable.begin(); iter != this->hashTable.end(); ++iter) {
    if (iter->second > max_result) {
        max_result = iter->second;
    }
}

哈希表复杂 key——自定义 Hashfunc 和 Equalfunc

Hashfunc 结构体需要重写()操作，主要是对复杂的 key 利用 hasher 进行哈希，注意要指定 seed
Equalfunc 结构体需要重写()操作，这个比较简单，确定两个 key 相同即可。
创建：unordered_map<vector<int>, int, Hashfunc, Equalfunc> hashTable

struct Hashfunc {
    size_t operator() (const vector<int> &key) const {
        std::hash<int> hasher;
        size_t seed = 0;
        for (int i: key) {
            seed ^= hasher(i) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
        }
        return seed;
    }
};

struct Equalfunc {
    bool operator() (const vector<int> &a, const vector<int> &b) const {
        if (a.size() != b.size()) {
            return 0;
        }
        for (int i = 0; i < a.size(); ++i) {
            if (a[i] != b[i]) {
                return 0;
            }
        }
        return 1;
    }
};

unordered_map<vector<int>, int, Hashfunc, Equalfunc> hashTable;

###

集合

unordered_map<int, set<int>> neighs;
unordered_map<int, set<int>>::iterator n_left_it = neighs.find(left);
if (n_left_it == neighs.end()) {
    set<int> r = {right};
    neighs[left] = r;
    // cout << "add left first" << left << " ";
    // print_vec(r);
} else {
    n_left_it->second.insert(right);
    // cout << "add left not first" << left << " ";
    // print_vec(r);
}

链表

核心思想 qia

链表是一种兼具递归和迭代性质的数据结构
递归的核心解法
- 回溯算法：后序遍历的重要性
- 例子：反转链表
迭代的核心解法
- 三指针法： pre、cur、next [始终一步一步地将 cur->next 设置为 pre，然后将 pre 设置为 cur，将 cur 设置为 next]
- 例子：k 个一组翻转；判断回文链表

反转链表

Leetcode 92：https://leetcode.cn/problems/reverse-linked-list-ii/submissions/

class Solution {
public:
    ListNode* backtrack(ListNode* head, int n) { // 模板: 反转前n个节点的链表!
        if (n == 1) {
            this->wait_next = head->next;
            return head;
        }

        ListNode* back = backtrack(head->next, n-1);

        // cout << "head: " << head->val << " ; back: " << back->val << endl;
        head->next->next = head;
        head->next = this->wait_next; // 之后会断掉, 目的是让第一个节点可以直接和最后相连
        return back;
    }
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        ListNode* dummy_head = new ListNode(-100); // 技巧: 增加一个节点
        dummy_head->next = head;
        ListNode* need_next = dummy_head;
        for (int i = 1; i < m; ++i) {
            need_next = need_next->next;
        }
        // cout << "check need_next: " << need_next->val << endl;
        

        ListNode* new_head = backtrack(need_next->next, n-m+1); 
        need_next->next = new_head;

        
        return dummy_head->next;
    }

private:
    ListNode* wait_next;
};

k 个一组反转链表

class Solution {
public:
    ListNode* reverse_a_b(ListNode* a, ListNode* b) { // 迭代方案
        ListNode* pre = nullptr;
        ListNode* cur = a;
        ListNode* nex = a;
        while (cur != b) { // [a, b)
            nex = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nex;
        }

        return pre; // 将头返回
    }
    ListNode* reverseKGroup(ListNode* head, int k) { // 递归方案
        ListNode* cur = head;
        for (int i = 0; i < k; ++i) {
            if (cur == nullptr) { // 不够就返回head
                return head;
            }
            cur = cur->next;
        }
        
        ListNode* new_head = reverse_a_b(head, cur);
        head->next = reverseKGroup(cur, k); // 很简洁的写法
        return new_head;   
    }
};

二叉树

核心思想

二叉树的前序遍历、中序遍历、后序遍历其实本质上等同于链表和数组的递归遍历思路

/* 迭代遍历数组 */
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {

    }
}

/* 递归遍历数组 */
void traverse(int[] arr, int i) {
    if (i == arr.length) {
        return;
    }
    // 前序位置
    traverse(arr, i + 1);
    // 后序位置
}

/* 迭代遍历单链表 */
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {

    }
}

/* 递归遍历单链表 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    // 前序位置
    traverse(head.next);
    // 后序位置
}

/* 递归遍历二叉树 */
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

针对链表：所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同：
针对二叉树：前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List：【你可以发现每个节点都有「唯一」属于自己的前中后序位置，所以我说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。】【二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。】
- 前序位置的代码在刚刚进入一个二叉树节点的时候执行；【很多题都是在前序位置写代码，实际上是因为我们习惯把那些对前中后序位置不敏感的代码写在前序位置罢了。】【前序位置的代码只能从函数参数中获取父节点传递来的数据！】
- 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。【中序位置主要用在 BST 场景中，你完全可以把 BST 的中序遍历认为是遍历有序数组。】
- 后序位置的代码在将要离开一个二叉树节点的时候执行；【主要的代码逻辑集中在后序位置：因为这个思路正确的核心在于，你确实可以通过子树的最大深度推导出原树的深度，所以当然要首先利用递归函数的定义算出左右子树的最大深度，然后推出原树的最大深度，主要逻辑自然放在后序位置。】【后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。】【一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。】

递归解题思路

二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题（分解成子树）计算出答案，这两类思路分别对应着回溯算法核心框架和动态规划核心框架。
- 在回溯算法核心框架中给出的函数签名一般也是没有返回值的 void backtrack(...)【一般还会涉及到做选择和撤销选择】
- 在动态规划核心框架中给出的函数签名是带有返回值的 dp 函数。

动态规划 / DFS / 回溯算法

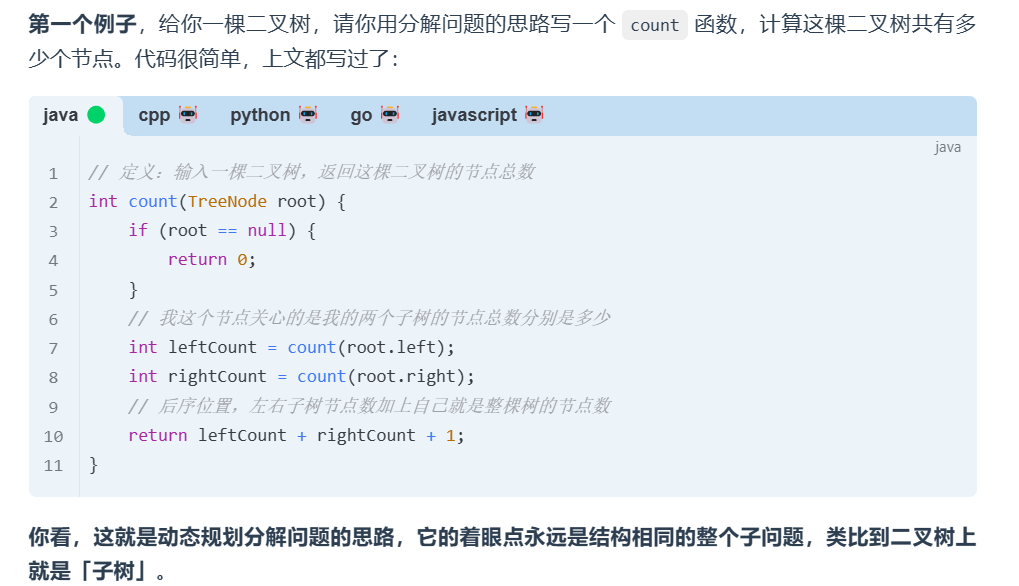
动态规划
- 分解问题的思路，关注点在子树！
- 例子：
  - Leetcode 100：https://leetcode.cn/problems/same-tree/description/?show=1
    - 前序遍历即可，注意参数需要传两个指针，这样可以一起进行遍历
  - Leetcode 101：https://leetcode.cn/problems/symmetric-tree/description/?show=1
    - 非常好的一道题目，还是 DP 的思想，让每个子树的两层满足部分情况即可!
    - 请多看题解：https://leetcode.cn/problems/symmetric-tree/solutions/46560/dong-hua-yan-shi-101-dui-cheng-er-cha-shu-by-user7/?show=1
  - Leetcode 1008：https://leetcode.cn/problems/construct-binary-search-tree-from-preorder-traversal/submissions/?show=1
    - 非常好的一道题目，从前序遍历的 vector 中恢复，因为本质上前序遍历就是找到一左一右，因此可以快速二分。二分后每次让子树去生成左右节点，因此这是一道 DP 的题目！
DFS
- 遍历的思路，关注点在节点！【似乎不关心走一条边多少次，关注的是节点访问的情况】
- 做选择和撤销选择的逻辑都在 for 循环外面

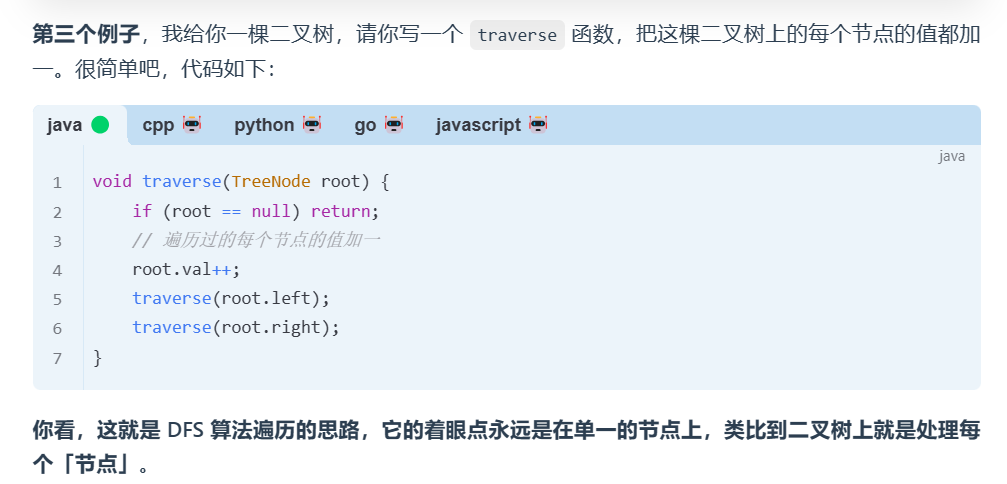
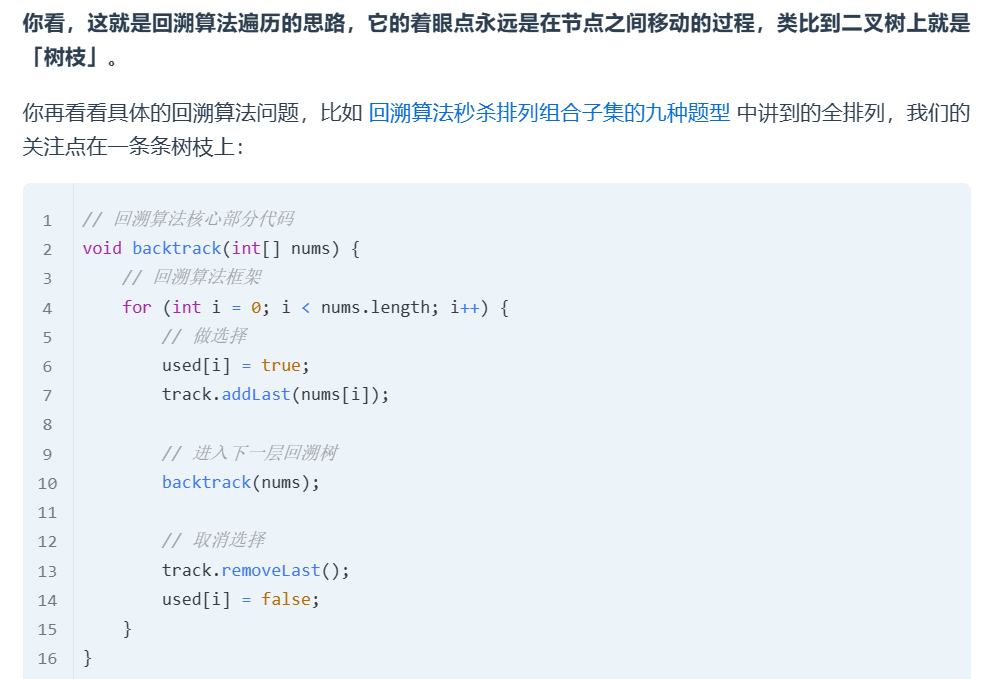
回溯算法
- 遍历的思路，关注点在树枝！【一般来说，走过的路还要走回来，所以说关注点在树枝】
- 做选择和撤销选择的逻辑都在 for 循环里面【因为需要拿到树枝的两个端点】

二叉树的深度后序框架[分解问题框架] + 其他 - Leetcode 543

class Solution {
public:
    int transver(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }
        
        int left_length = transver(root->left);
        int right_length = transver(root->right);
        

        int result_length = left_length + right_length;

        if (result_length > this->max_length) {
            this->max_length = result_length;
        }
        return 1 + max(left_length, right_length);
    }
    int diameterOfBinaryTree(TreeNode* root) {
        int temp_result = transver(root);
        return this->max_length;
    }
private:
    int max_length = 0;
};

完美二叉树的三叉树化：可以用于对同层的不同子树进行连接

Leetcode 116
- 参考文献：https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-66994/dong-ge-da-cbce8/

// 注意：cpp 代码由 chatGPT🤖 根据我的 java 代码翻译，旨在帮助不同背景的读者理解算法逻辑。
// 本代码不保证正确性，仅供参考。如有疑惑，可以参照我写的 java 代码对比查看。

// 主函数
Node* connect(Node* root) {
    if (root == nullptr) return nullptr;
    // 遍历「三叉树」，连接相邻节点
    traverse(root->left, root->right);
    return root;
}

// 三叉树遍历框架
void traverse(Node* node1, Node* node2) {
    if (node1 == nullptr || node2 == nullptr) {
        return;
    }
    /**** 前序位置 ****/
    // 将传入的两个节点穿起来
    node1->next = node2;
    
    // 连接相同父节点的两个子节点
    traverse(node1->left, node1->right);
    traverse(node2->left, node2->right);
    // 连接跨越父节点的两个子节点
    traverse(node1->right, node2->left);
}

DFS

Leetcode 1457

/**
Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
 */

#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    bool checkHuiwen(unordered_map<int, int> &umap) {
        bool has_one_single = false;
        for (unordered_map<int, int>::iterator iter = umap.begin(); iter != umap.end(); ++iter) {
            if (iter->second % 2 && !has_one_single) {
                has_one_single = true;
            } else if (iter->second % 2 && has_one_single) {
                return false;
            }
        }
        return true;
    }
    int preTransver(TreeNode* root, int result, unordered_map<int, int> &umap) {
        cout << "check root->val [add one]: " <<  root->val << endl;
        umap[root->val] += 1;
        if (root->left == NULL && root->right == NULL) {
            if (checkHuiwen(umap)) {
                cout << "is hui wen" << endl;
                
                return result + 1;
            } else {
                cout << "not is hui wen" << endl;
                // umap[root->val] -= 1;
                return result;
            }
        }
        
        if (root->left) {
            result = preTransver(root->left, result, umap);
            umap[root->left->val] -= 1;
            cout << "[sub one]: " << root->left->val << endl;
        }
        
        if (root->right) {
            result = preTransver(root->right, result, umap);
            umap[root->right->val] -= 1;
            cout << "[sub one]: " << root->right->val << endl;
        }
        
        return result;

    }
    int pseudoPalindromicPaths (TreeNode* root) {
        unordered_map<int, int> umap;
        int result = preTransver(root, result, umap);
        return result;
    }
};

int main() {
    TreeNode *root = new TreeNode(2);
    root->left = new TreeNode(1);
    root->right = new TreeNode(1);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(3);
    root->left->right->right = new TreeNode(1);

    Solution *sol = new Solution();

    int result = sol->pseudoPalindromicPaths(root);
    cout << result << endl;
}

BFS (可以用分层 next 链表去替代 queue)

Leetcode 116/117：填充每个节点的下一个右侧节点指针
经典 BFS：严重依赖于 queue！

Node* connect(Node* root) {
    queue<Node*> q;
    q.push(root);

    int level = 1;
    int next_level = 0;
    while (!q.empty()) {
        Node *current_pointer = q.front();
        q.pop();

        if (current_pointer == NULL) {
            continue;
        }
        if (current_pointer->left) {
            q.push(current_pointer->left);
            next_level += 1;
        }
        if (current_pointer->right) {
            q.push(current_pointer->right);
            next_level += 1;
        }
        for (int i = 0; i < level - 1; ++i) {
            cout << "set current_pointer: " << current_pointer->val << " to next: " << q.front()->val << endl;
            current_pointer->next = q.front();
            q.pop();

            current_pointer = current_pointer->next;

            if (current_pointer->left) {
                q.push(current_pointer->left);
                next_level += 1;
            }
            if (current_pointer->right) {
                q.push(current_pointer->right);
                next_level += 1;
            }
        }
        cout << "next_level: " << next_level << endl;
        level = next_level;
        next_level = 0;
    }
    return root;
}

利用链表模拟

Node* connect(Node* root) {
    if (root == NULL) {
        return root;
    }
    if (root->left != NULL && root->right != NULL) {
        root->left->next = root->right;
    }
    Node *cur;
    if (root->left != NULL) {
        cur = root->left;
    } else {
        cur = root->right;
    }

    while (cur != NULL) {
        Node *head = new Node(-1);
        Node *tail = head;
        for (; cur != NULL; cur = cur->next) {
            if (cur->left != NULL) {
                // cout << "set tail: " << tail->val << " next: " << cur->left->val << endl;
                tail->next = cur->left;
                tail = tail->next;
            }
            if (cur->right != NULL) {
                // cout << "set tail: " << tail->val << " next: " << cur->right->val << endl;
                tail->next = cur->right;
                tail = tail->next;
            }
        }
        cur = head->next;
    }
    return root;
}

前序遍历 (总是先判断根节点再处理子节点)

// 前序遍历, 总是先走到最左端点再回来
int front_transve(TreeNode* root, int up, int down, int result) {
    if (root == nullptr) {
        return up - down;
    }
    
    up = max(up, root->val);
    down = min(down, root->val);
    

    int left_result = front_transve(root->left, up, down, result);
    int right_result = front_transve(root->right, up, down, result);
    result = max(max(left_result, right_result), up-down);

    return result;
}

后序遍历 (总是先判断两个子节点再处理根节点)

一些二叉树搜索操作很常见
题型：根据某些条件删除二叉树的部分节点、根据某些条件拆分二叉树、根据子节点的统计信息处理根节点

// 1110. 删点成林
class Solution {
public:
    void backTransver(TreeNode* root, TreeNode* parent, bool left, vector<TreeNode*>& result, vector<int>& to_delete) {
        if (root == nullptr) {
            return ;
        }
        if (root->left) {
            backTransver(root->left, root, true, result, to_delete);
        }
        if (root->right) {
            backTransver(root->right, root, false, result, to_delete);
        }

        if (find(to_delete.begin(), to_delete.end(), root->val) != to_delete.end()) {
            if (root->left) {
                result.push_back(root->left);
            }
            if (root->right) {
                result.push_back(root->right);
            }
            if (parent != nullptr) {
                if (left) {
                    parent->left = nullptr;
                } else {
                    parent->right = nullptr;
                }
            }
        }
    }
    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        vector<TreeNode*> result = {};
        if (root != nullptr && find(to_delete.begin(), to_delete.end(), root->val) == to_delete.end()) {
            result.push_back(root);
        }
        backTransver(root, nullptr, false, result, to_delete);

        return result;
    }
};

回溯算法

选择-递归-撤销选择的思路

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

和 DFS 的区别

回溯算法：关心的是边，选择和撤销发生在 for 循环内部
DFS：关心的节点，选择和撤销发生在 for 循环外部

回溯算法的分类

子集 [元素没有重复、元素不可以重复选]

剪枝法

void backtrack(int n, int k, int start, vector<int>& path, vector<vector<int>>& result) {
    // 每个path都要被采用
    result.push_back(path);

    for (int i = start; i <= n; ++i) {
        // 选择
        path.push_back(i);
        
        backtrack(n, k, i+1, path, result);

        // 撤销选择
        path.pop_back();
    }
}

组合 [元素没有重复、元素不可以重复选]

剪枝法

void backtrack(int n, int k, int start, vector<int>& path, vector<vector<int>>& result) {
    if (path.size() == k) {
        result.push_back(path);
        return;
    } else if (path.size() > k) {
        return;
    }

    for (int i = start; i <= n; ++i) {
        // 选择
        path.push_back(i);
        
        backtrack(n, k, i+1, path, result);

        // 撤销选择
        path.pop_back();
    }
}

排列 [元素没有重复、元素不可以重复选]

需要 flag 数组标记【注意，如果是类似 N 皇后那种只用两种状态无法表征的情况，则需要使用 int 类型的数组】

void backtrack(vector<int>& nums, bool* used_flag, vector<int>& path, vector<vector<int>>& result) {
    if (path.size() == nums.size()) {
        result.push_back(path);
        return;
    }
    for (int i = 0; i < nums.size(); ++i) {
        if (used_flag[i]) {
            continue;
        }

        // 做决定
        path.push_back(nums[i]);
        used_flag[i] = true;
        
        backtrack(nums, used_flag, path, result);
        // 撤销决定
        path.pop_back();
        used_flag[i] = false;
    }
}

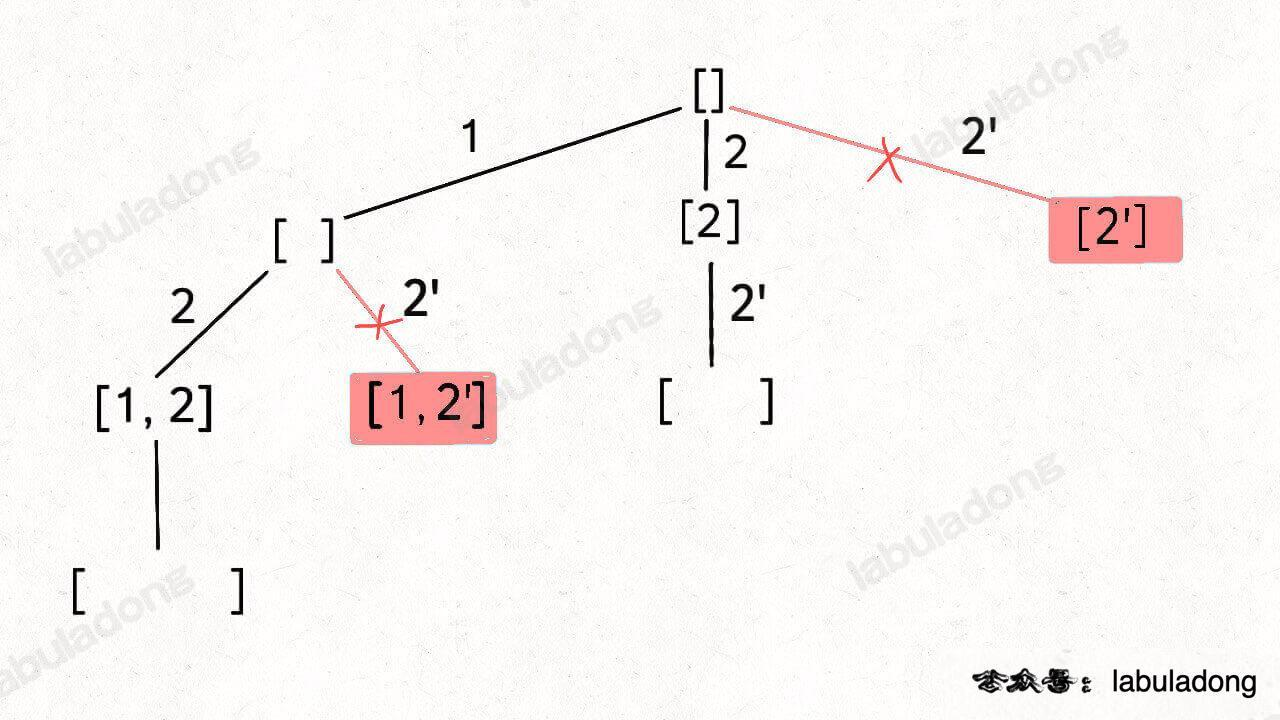
子集 / 组合 [元素有重复、元素不可以重复选]

for 循环的时候，遇到相同的就不走了！所以判断条件是那样子

class Solution {
public:
    void backtrack(int start, vector<int>& nums, vector<int>& path, vector<vector<int>>& result) {
        result.push_back(path);

        for (int i = start; i < nums.size(); ++i) {
            if (i > start && nums[i] == nums[i-1]) { 
                // 不能是第一个，因为不能和start-1比较
                continue;
            }

            path.push_back(nums[i]);
            
            backtrack(i+1, nums, path, result);

            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int start = 0;
        vector<int> path = {};
        vector<vector<int>> result = {};
        // 排序后正常剪枝?
        backtrack(start, nums, path, result);
        return result;
    }
};

排列 [元素有重复、元素不可以重复选]

将重复元素剔除掉，同时还要保证顺序不乱？
- 顺序不乱的要求：前一个元素需要用过才会进入？

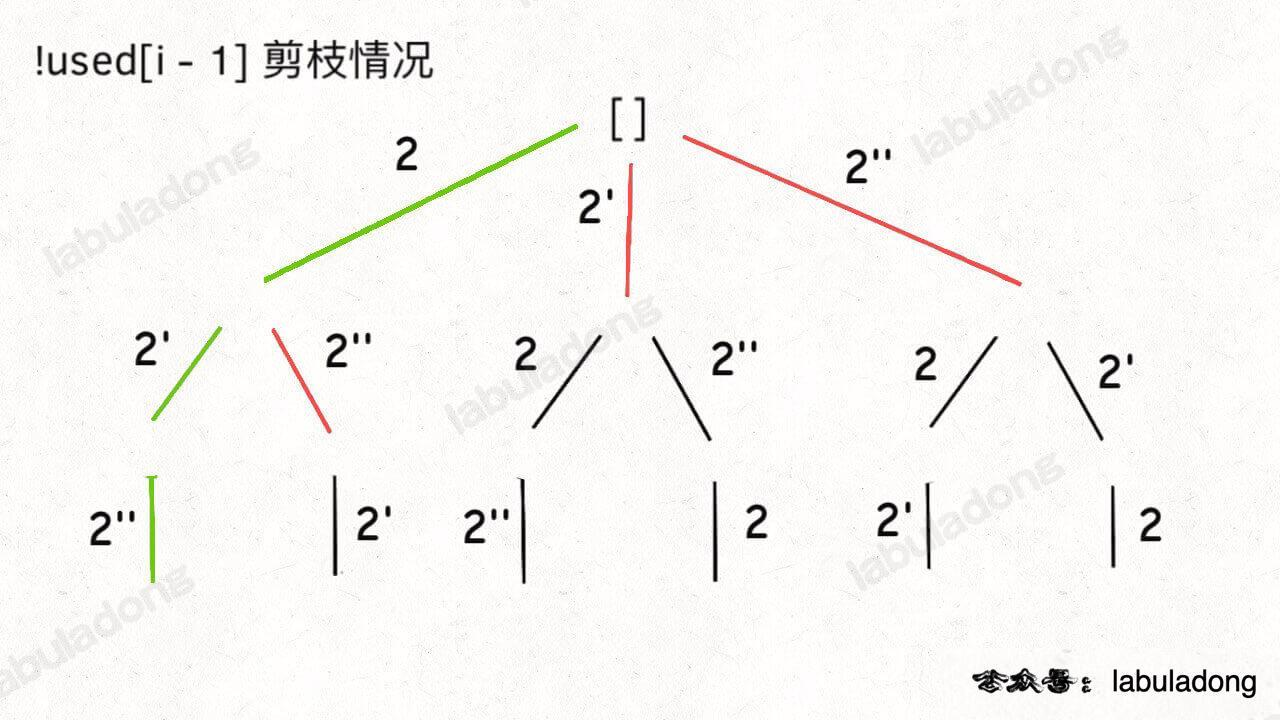
class Solution {
public:
    void backtrack(vector<int>& nums, vector<vector<int>>& result, vector<int>& path, vector<bool>& used_flag) {
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }

        for (int i = 0; i < nums.size(); ++i) {
            if (i > 0 && nums[i] == nums[i-1] && !used_flag[i-1]) {
                continue;
            }
            if (used_flag[i]) {
                continue;
            }

            // jueding 
            path.push_back(nums[i]);
            used_flag[i] = true;
            
            backtrack(nums, result, path, used_flag);
            // chexiao jueding
            path.pop_back();
            used_flag[i] = false;
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> result = {}; 
        vector<int> path = {}; 
        vector<bool> used_flag = {};
        for (int i = 0; i < nums.size(); ++i) {
            used_flag.push_back(false);
        }
        backtrack(nums, result, path, used_flag);
        return result;
    }
};

组合 [元素没有重复、元素可以被重复选]

进入递归的时候，传入 i 可以重复选这个项目！

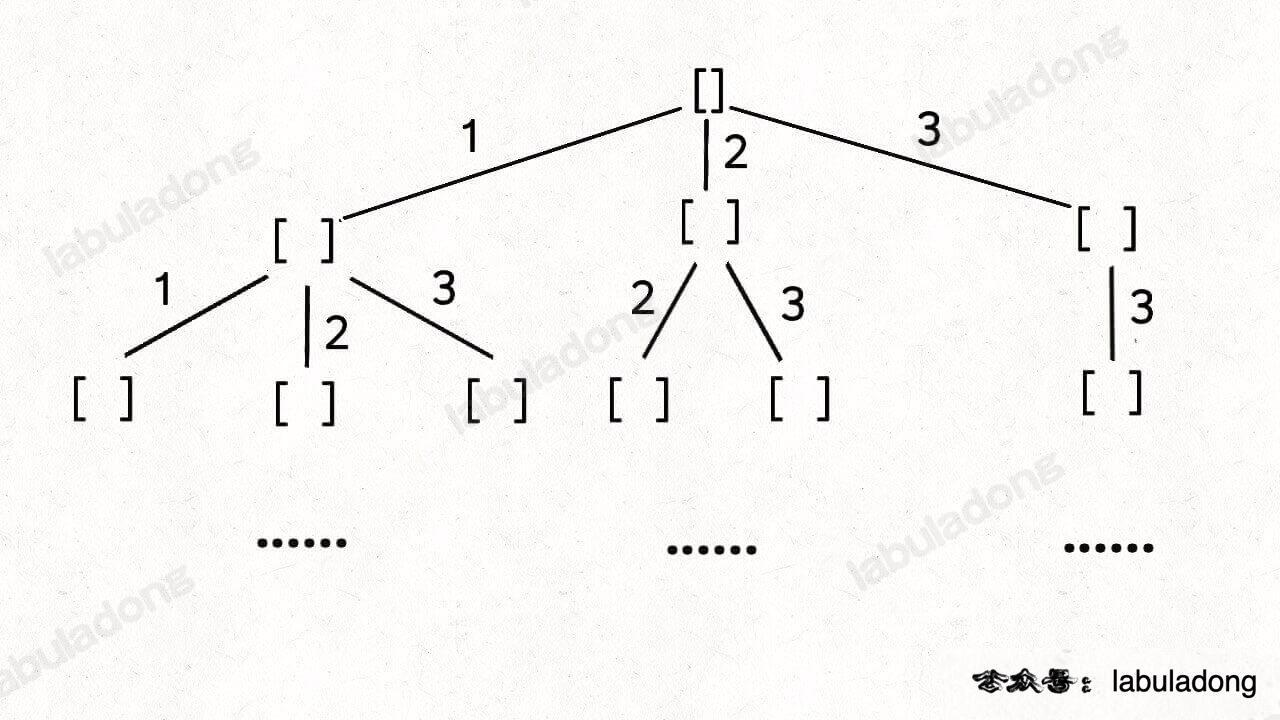
class Solution {
public:
    void backtrack(vector<int>& candidates, int target, vector<vector<int>>& result, vector<int>& path, int path_sum, int start) {
        if (path_sum > target) {
            return;
        } else if (path_sum == target) {
            result.push_back(path);
            return;
        }

        for (int i = start; i < candidates.size(); ++i) {
            path.push_back(candidates[i]);
            path_sum += candidates[i];

            backtrack(candidates, target, result, path, path_sum, i); // 下次还从i的位置开始还能接着选

            path.pop_back();
            path_sum -= candidates[i];
        }
        
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end(), greater<int>());
        vector<vector<int>> result = {}; 
        vector<int> path = {}; 
        int path_sum = 0;
        int start = 0;
        backtrack(candidates, target, result, path, path_sum, start);
        return result;
    }
};

例子: Leetcode 51 N 皇后

注意：状态可能 bool 状态无法完全表达，因为 2 元状态机可能撤销的时候会被覆盖！

class Solution {
public:
    void transve(vector<vector<string>>& result, vector<string>& path, vector<vector<int>>& flag, string& new_line, int row_id, int n) {
        // cout << "whta?" << endl;
        if (row_id >= n) {
            result.push_back(path);
            return;
        }
        
        for (int i = 0; i < n; ++i) {
            if (flag[row_id][i] > 0) {
                continue;
            }

            // 选择
            
            new_line[i] = 'Q';
            // cout << "check new_line: " << new_line << endl;
            path.push_back(new_line);
            new_line[i] = '.';
            
            // i列, (row_id++, i++)
            for (int j = row_id + 1; j < n; ++j) {
                flag[j][i] += 1;
            }
            for (int j = row_id + 1, k = i + 1; j < n && k < n; ++j, ++k) {
                flag[j][k] += 1;
            }
            for (int j = row_id + 1, k = i - 1; j < n && k >= 0; ++j, --k) {
                flag[j][k] += 1;
            }

            transve(result, path, flag, new_line, row_id+1, n);

            // 撤销选择
            path.pop_back();
            for (int j = row_id + 1; j < n; ++j) {
                flag[j][i] -= 1;
            }
            for (int j = row_id + 1, k = i + 1; j < n && k < n; ++j, ++k) {
                flag[j][k] -= 1;
            }
            for (int j = row_id + 1, k = i - 1; j < n && k >= 0; ++j, --k) {
                flag[j][k] -= 1;
            }
        }
    }
    vector<vector<string>> solveNQueens(int n) {
        // cout << "what?" << endl;
        vector<vector<string>> result = {}; 
        vector<string> path = {};
        vector<vector<int>> flag = {};
        char ch = '.';
        string new_line(n, ch);
        for (int i = 0; i < n; ++i) {
            vector<int> line = {};
            flag.push_back(line);
            for (int j = 0; j < n; ++j) {
                flag[i].push_back(0);
            }
        } 
        int row_id = 0;
        
        transve(result, path, flag, new_line, row_id, n);
        return result;
    }
};

例子: Leetcode 78 返回全排列组合

class Solution {
public:
    void backtrack(vector<int>& nums, vector<int>& path, vector<vector<int>>& result, int start) {
        result.push_back(path);
        if (path.size() >= nums.size()) {
            return;
        }

        for (int i = start; i < nums.size(); ++i) {
            path.push_back(nums[i]);

            backtrack(nums, path, result, i+1); // 剪枝树, 避免重复计算

            path.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<int> path = {}; 
        vector<vector<int>> result = {};
        int start = 0;

        backtrack(nums, path, result, start);
        return result;
    }
};

遍历 for

auto 智能指针

for (const auto x: arr) {
    cout << x << endl;
}

Tuple

一个避免使用 struct 的简易数据结构，可以用 std::tuple 进行初始化，并用 std::tie 进行解包

#include<iostream>
#include<tuple>
#include<string>

int main() {
    // 感觉是一个不错的东西, 可以避免使用struct构造, 方便!
    std::tuple<int, double, std::string> t3 = {1, 2.0, "3"}; // 初始化
    std::cout << std::get<0>(t3) << std::endl;

    int i;
    double j;
    std::string k;
    std::tie(i, j, k) = t3; // 解包
    std::cout << "i: " << i << "; j: " << j << "; k: " << k << std::endl;
}

C++ 的 deque

双端队列，使用两个双端队列可以用在滑动窗口中以非常低的成本来快速维护窗口中局部的 Max 和 Min
方法：用一个 Max queue 保存最大值和比最大值小一些的量，直到窗口滑到一个比最大值还大的量，则抛弃之前的保存值；Min queue 也是同理。
https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/solution/gai-zhuang-ban-hua-dong-chuang-kou-liang-271k/

class Solution {
public:
    int longestSubarray(vector<int>& nums, int limit) {
        deque<int> min_heap;
        deque<int> max_heap;
        

        int l = 0;
        int r = 0;
        int res = 0;
        int count = nums.size();

        while (r < count) {
            while (!max_heap.empty() && max_heap.front() < nums[r]) {
                max_heap.pop_front(); // 只有当右边新来的item比维护的最大值大的时候, 需要删除所有内容
            }
            while (!min_heap.empty() && min_heap.front() > nums[r]) {
                min_heap.pop_front(); // 只有当右边新来的item比维护的最小值小的时候，需要删除所有内容
            }

            // 两个deque合并在一起就是当前窗口的内容，其中最大值的位置会有两个值

            max_heap.push_back(nums[r]);
            min_heap.push_back(nums[r]);

            r++;
            
            while (max_heap.front() - min_heap.front() > limit) { // 判断条件! 可以自定义
                if (max_heap.front() == nums[l]) {
                    max_heap.pop_front();
                }
                if (min_heap.front() == nums[l]) {
                    min_heap.pop_front();
                }
                l++;
            }

            res = max(res, r-l);
        }
        
        // cout << "min_heap: " << min_heap.top() << endl;
        // cout << "max_heap: " << max_heap.top() << endl;
        return res;
    }
};

C++11 整个专题

lambda

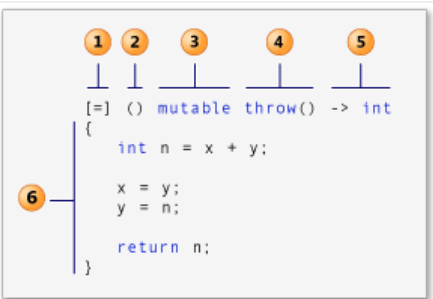
这是一个比较大的坑，在 C++11 引入 lambda 函数，后续在 C++14 引入了泛型。
function< 返回值类型(参数类型)> = & -> 返回值类型 {}
1. capture 子句（在 C++ 规范中也称为 Lambda 引导。）
2. 参数列表（可选）。（也称为 Lambda 声明符）
3. mutable 规范（可选）。
4. exception-specification（可选）。
5. trailing-return-type（可选）。
6. Lambda 体。
[] 中的内容表示不同的 capture 子句：Lambda 可在其主体中引入新的变量（用 C++14），它还可以访问（或“捕获”）周边范围内的变量。 Lambda 以 capture 子句开头。它指定捕获哪些变量，以及捕获是通过值还是通过引用进行的。
- 有与号 (&) 前缀的变量通过引用进行访问，没有该前缀的变量通过值进行访问。
- 空 capture 子句 [ ] 指示 lambda 表达式的主体不访问封闭范围中的变量。
- 可以使用默认捕获模式来指示如何捕获 Lambda 体中引用的任何外部变量：[&] 表示通过引用捕获引用的所有变量，而 [=] 表示通过值捕获它们。
- 可以使用默认捕获模式，然后为特定变量显式指定相反的模式。例如，如果 lambda 体通过引用访问外部变量 total 并通过值访问外部变量 factor，则以下 capture 子句等效：

[&total, factor]
[factor, &total]
[&, factor]
[=, &total]

struct Node {
    int time;
    vector<Node*> childs;

    Node(int time) {
        this->time = time;
        this->childs = {};
    }

    void add_child(Node* child) {
        // cout << "add " << child->id << " into " << this->id << endl;
        this->childs.push_back(child);
    }
};

class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        // build tree
        vector<Node*> id_tree_vec = {};
        for (int id = 0; id < n; ++id) {
            Node* node = new Node(informTime[id]);
            id_tree_vec.push_back(node);
        }
        
        for (int id = 0; id < n; ++id) {
            int manager_id = manager[id];
            if (manager_id != -1) {
                id_tree_vec[manager_id]->add_child(id_tree_vec[id]);
            }
        }

        function<int(Node*)> rec = [&](Node* root) -> int {
            if (root->childs.size() <= 0) {
                return 0;
            }
            
            int max_child_result = -9999999;
            for (Node* c: root->childs) {
                max_child_result = max(max_child_result, rec(c));
            }
            // cout << "in " << root->id << " max_child_result: " << max_child_result << endl;
            return root->time + max_child_result;
        };
        // cout << "finished!" << id_tree_vec[headID]->id << endl;
        int result = rec(id_tree_vec[headID]);
        return result;
    }
};

动态规划

Leetcode 1039：切分三角形

class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int size = values.size();
        vector<vector<int>> dp(size, vector<int>(size));
        for (int step = 2; step < size; ++step) {
            // cout << "[step: " << step << "]" << endl;
            for (int i = 0; i < size - step; ++i) {
                // cout << "enter: i[" << i << endl;
 
                int temp = 9999999;
                for (int k = i + 1; k < i + step; ++k) {
                    if (i + step < size) {
                        temp = min(dp[i][k] + dp[k][i+step] + values[i] * values[k] * values[i+step], temp);
                        // cout << "dp[i][k]: " << dp[i][k] << endl;
                        // cout << "dp[k][i+step]: " <<  dp[k][i+step] << endl;
                        // cout << "values[i] * values[k] * values[i+step]:" << values[i] * values[k] * values[i+step] << endl;
                        // cout << "jisuan: " << dp[i][k] + dp[k][i+step] + values[i] * values[k] * values[i+step] << endl;
                        // cout << "[i: " << i << "; k: " << k << "; i+step: " << i + step << "]: " << temp << endl;
                    }
                }
                // printf("set: dp[%d][%d]: %d\n", i, i+step, temp);
                dp[i][i+step] =  temp;
                
            }
        }
        return dp[0][size-1];
    }
};

Leetcode 2304：网格中的最小路径代价

暴力 DP：

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
        vector<vector<int>> dp;
        int row_num = grid.size();
        int col_num = grid[0].size();
        for (int i = 0; i < row_num; ++i) {
            vector<int> line_result = {};
            dp.push_back(line_result);
            for (int j = 0; j < col_num; ++j) {
                dp[i].push_back(0);
            }
        }

        for (int j = 0; j < col_num; ++j) {
            dp[0][j] = grid[0][j];
        }

        int MAX_NUM = 1410065404;
        for (int i = 1; i < row_num; ++i) {
            for (int j = 0; j < col_num; ++j) {
                int min_dp = MAX_NUM;
                for (int m = 0; m < col_num; ++m) {
                    // cout << "forward is (i - 1): " << i - 1 << " m: " << m << " moveCost[grid[i-1][m]][j]: " << moveCost[grid[i-1][m]][j] << endl;
                    if (dp[i-1][m] + grid[i][j] + moveCost[grid[i-1][m]][j] < min_dp) {
                        min_dp = dp[i-1][m] + grid[i][j] + moveCost[grid[i-1][m]][j];
                    }
                    
                }

                dp[i][j] = min_dp;
                // cout << "to i: " << i << " j: " << j << " dp value: " << dp[i][j] << endl;
            }
        }

        int result = MAX_NUM;
        for (int j = 0; j < col_num; ++j) {
            if (dp[row_num-1][j] < result) {
                result = dp[row_num-1][j];
            }
        }
        return result;
    }
};

优化：原地修改【直接从下到上！！！】

BFS

Leetcode 2451
BFS 很适合确定层数！

贪心算法

Leetcode 1053 更换顺序字典序最小序列

class Solution {
public:
    vector<int> prevPermOpt1(vector<int>& arr) {
        if (arr.size() == 1) {
            return arr;
        } else if (arr.size() == 2) {
            if (arr[0] > arr[1]) {
                swap(arr[0], arr[1]);
            }
            return arr;
        } else {
            int last_one_up = 99999;
            int last_index = arr.size() - 1;
            while (last_index >= 0 && arr[last_index] <= last_one_up) {
                last_one_up = arr[last_index];
                last_index -= 1;
            }
            if (last_index < 0) {
                return arr;
            } else {
                last_one_up = arr[last_index];
            }
            int second_index = arr.size() - 1;
            while (second_index > last_index && arr[second_index] >= last_one_up) {
                // cout << "arr[second_index]: " << arr[second_index] << "; last_one_up: " << last_one_up << endl; 
                --second_index;
            }
            int second_one_up = arr[second_index];
            while (second_index - 1 > last_index && arr[second_index - 1] == second_one_up) {
                --second_index;
            }
            // cout << "last_index: " << last_index << "; second_index: " << second_index << endl; 
            swap(arr[last_index], arr[second_index]);
            return arr;
        }
    }
    
    int a=1;
    int b=3;
    cont<<"KFC V me 50"<<endl;
};

Leetcode 1042 着色问题

1042. 不邻接植花 - 力扣（LeetCode）
这个贪心用的非常直接，而且算法还是比较暴力且考验各种数据结构的熟练程度，是一个不错的代码

Leetcode 2517 最大最小优化问题

https://leetcode.cn/problems/maximum-tastiness-of-candy-basket/
这就是一个非常经典的最大最小优化问题

Leetcode 2611 两方离线资源分配问题

这个题很简单，但是自己想却想不出来……
思路就是计算所有资源分配给 1 和分配给 2 的 utility 差值，然后从高到低排序即可！但是如果搜索算法的效率就会很低，但是贪心直接就得到了最优解！

bool cmp(const int &a, const int &b) { 
    return a > b;
}

class Solution {

public:
    int miceAndCheese(vector<int>& reward1, vector<int>& reward2, int k) {
        
        for (int i = 0; i < reward1.size(); ++i) {
            reward1[i] = reward1[i] - reward2[i];
        }

        sort(reward1.begin(), reward1.end(), cmp);
        

        int result = 0;
        for (int i = 0; i < k; ++i) {
            result += (reward1[i] + reward2[i]);
        }
        for (int i = k; i < reward1.size(); ++i) {
            result += reward2[i];
        }

        return result;
    }
};

单调栈

Leetcode 1019 获取链表的下一个更大的值

package main

import (
    "fmt"
    "sync"
)

type ListNode struct {
    Val  int
    Next *ListNode
}

type Item struct {
    OriginIndex int
    Val         int
}
type ItemStack struct {
    items []Item
    lock  sync.RWMutex
}

func NewStack() *ItemStack {
    s := &ItemStack{}  // 初始化Stack
    s.items = []Item{} // 初始化数组
    return s
}

func (s *ItemStack) Print() {
    fmt.Println(s.items)
}

func (s *ItemStack) Push(t Item) {
    s.lock.Lock()
    defer s.lock.Unlock()
    // fmt.Println("push t: ", t)
    s.items = append(s.items, t)
}

func (s *ItemStack) Pop() {
    s.lock.Lock()
    defer s.lock.Unlock()
    if len(s.items) == 0 {
        return
    }
    index := len(s.items) - 1
    // item := s.items[index]
    // fmt.Println("pop t: ", item)
    s.items = s.items[0:index]
    // fmt.Println("success pop !")
}

func (s *ItemStack) Top() *Item {
    s.lock.Lock()
    defer s.lock.Unlock()

    // fmt.Println("get index")
    if len(s.items) == 0 {
        return nil
    }
    index := len(s.items) - 1

    item := s.items[index]
    // fmt.Println("success top !")
    return &item
}

func (s *ItemStack) Len() int {
    return len(s.items)
}

func transver(head *ListNode) {
    for head != nil {
        fmt.Println(head.Val)
        head = head.Next
    }
}

func nextLargerNodes(head *ListNode) []int {
    stack := NewStack()

    var index = 0
    var res []int
    for head != nil {
        if stack.Len() == 0 {
            var item Item
            item.OriginIndex = index
            item.Val = head.Val
            stack.Push(item)
            // fmt.Println("current stack: ", stack.items)
        } else {
            top_item := stack.Top()
            for top_item != nil && head.Val > top_item.Val {
                // fmt.Println("pop_item: ", top_item.Val, " head.Val: ", head.Val)
                stack.Pop()
                res[top_item.OriginIndex] = head.Val
                top_item = stack.Top()
                // fmt.Println("next top_item: ", top_item)
            }
            var item Item
            item.OriginIndex = index
            item.Val = head.Val
            stack.Push(item)
            // fmt.Println("current stack: ", stack.items)
        }
        res = append(res, 0)
        index = index + 1
        head = head.Next
    }
    return res
}

func main() {
    var head = new(ListNode)
    head.Val = 2

    var second = new(ListNode)
    second.Val = 7
    head.Next = second

    var third = new(ListNode)
    third.Val = 4
    second.Next = third

    var fourth = new(ListNode)
    fourth.Val = 3
    third.Next = fourth

    var fifth = new(ListNode)
    fifth.Val = 5
    fourth.Next = fifth

    result := nextLargerNodes(head)
    fmt.Println(result)
}

【请复习】Leetcode 907 子数组的最小值之和

参考文献：https://lfool.github.io/LFool-Notes/algorithm/%E5%8D%95%E8%B0%83%E6%A0%88-%E6%8B%93%E5%B1%95%E5%BA%94%E7%94%A8.html

数论

负二进制模拟

这是一个在 KTV 写的题，当时没有写出来，现在回想一下还是比较简单的。
第一步，先要将十进制数进行二进制分解
- 27 => 16 + 8 + 2 + 1
第二步，将这些数中无法在二进制中取得负数的值转化一下
- 8 = 16 + (-8)
- 2 = 4 + (-2)
第三步，从低位到高位将转化后的二进制数组写出来，slice 中第一位表示负二进制数，第二位表示出现的次数
- [(1, 1), (-2, 1), (4, 1), (-8, 1), (16, 2)]
第四步，对出现大于等于 2 和小于等于-1 的情况进行处理
- 大于等于 2：当前位减去 2，高一位减去 1
- 小于等于-1：当前位加上 2，高一位加上 1
第五步，一个 while 循环，直到最高位置出现的数量为 0 或 1 结束即可！

双指针

链表中的双指针：
- 中间相差 k 可以获取从前后开始的第 k 个节点 - https://leetcode.cn/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/
- 快指针走 2 步，慢指针走 1 步：可以在不知道 n 的情况下获得中点的位置！ - https://leetcode.cn/problems/middle-of-the-linked-list/
- 快指针走 2 步，慢指针走 1 步：可以判断一个链表是否成环！【因为只要有环，肯定会让快慢指针重合的，没有环肯定就直接走了！】
- 同速指针：找到两个链表的相交 node！！【同时应该考虑链表的长度~】
数组中的双指针
- 左右窗口双指针：用于左右压缩空间
- 快慢双指针：一般是一个指针比较快，另一个指针比较慢，一般是用于原地覆盖 nums！！

LCR. 140 链表的倒数第 k 个 node - 快慢指针

快慢指针，快指针比慢指针多走 k 步，最后快指针到 null 的时候，倒数第 k 个就慢指针的位置。

class Solution {
public:
    ListNode* trainingPlan(ListNode* head, int cnt) {
        ListNode* fast = head;
        ListNode* slow = head;

        for (int i = 0; i < cnt; ++i) {
            fast = fast->next;
        }

        while (fast != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

Leetcode 1410 字符串匹配和替换

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    string entityParser(string text) {
        unordered_map<string, string> umap;
        
        umap["&quot;"] = "\"";
        umap["&apos;"] = "\'";
        umap["&amp;"] = "&";
        umap["&gt;"] = ">";
        umap["&lt;"] = "<";
        umap["&frasl;"] = "/";

        int left = 0;
        int right = 0;
        bool left_fix = false;
        bool right_fix = false;
        int to_copy_str_index = 0;
        string result = "";
        for (int i = 0; i < text.length(); ++i) {
            if (text[i] == '&') {
                left = i;
                left_fix = true;
                // cout << "left: " << left << endl; 
            }
            if (text[i] == ';' && left_fix) {
                right = i;
                right_fix = true;
                // cout << "right: " << right << endl; 
            }
            if (left_fix && right_fix && left < text.length() && right < text.length()) {
                string need_judge_substr = text.substr(left, right - left + 1);

                // cout << "need_judge_substr: " << need_judge_substr << endl; 
                unordered_map<string, string>::iterator iter = umap.find(need_judge_substr);
                if (iter != umap.end()) {
                    int to_copy_len = left - to_copy_str_index;
                    for (int q = to_copy_str_index; q < to_copy_str_index + to_copy_len; ++q) {
                        result += text[q];
                    }
                    result += iter->second;
                    
                    to_copy_str_index = right + 1;
                    left_fix = false;
                    right_fix = false;
                } else {
                    left_fix = false;
                    right_fix = false;
                }
            }
            
        }
        if (to_copy_str_index < text.length()) {
            int to_copy_len = text.length() - to_copy_str_index;
            for (int q = to_copy_str_index; q < to_copy_str_index + to_copy_len; ++q) {
                result += text[q];
            }
        }
        return result;
    }
};

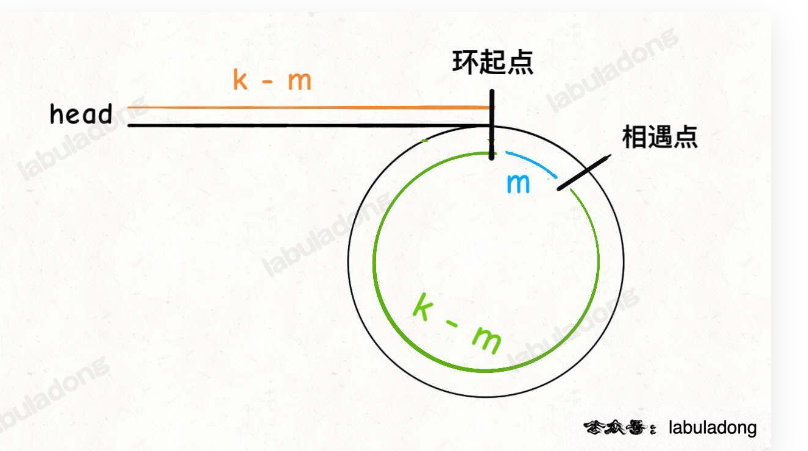
Leetcode 142 环形链表 II

这道题真的是双指针的代表性题目
- 先变速指针：相遇之后，快指针走 2k 步，慢指针走 k 步。其中 k 肯定是环的倍数！
- 后同速指针：那么从 head 到相遇点是 k，整个环也是 k，因此可以从数学上获得入环的起点！

Leetcode 5 最长回文子串

尽量记住，子串一般使用双指针！
这道题的思路应该是从中间开始向左右指针，这样复杂度每个都可以压倒 O(n)，总共需要外层训练 O(n)次，复杂度是 O(n^2)

class Solution {
public:
    vector<int> test(string &s, int i, int j) {
        while (i >= 0 && j < s.size() && s[i] == s[j]) {
            i--;
            j++;
        }
        int len = (j - 1) - (i + 1) + 1;
        vector<int> res;
        res.push_back(i+1);
        res.push_back(len);
        // cout << "push: " << i+1 << " " << len << endl;
        return res;
    }
    string longestPalindrome(string s) {
        int max_len = -1;
        vector<int> res = {-1, -1};

        for (int i = 0; i < s.size(); ++i) {
            vector<int> sub_str_0 = test(s, i, i);
            vector<int> sub_str_1 = test(s, i, i+1);

            if (sub_str_0[1] > max_len) {
                res[0] = sub_str_0[0];
                res[1] = sub_str_0[1];
                max_len = res[1];
            }
            if (sub_str_1[1] > max_len) {
                res[0] = sub_str_1[0];
                res[1] = sub_str_1[1];
                max_len = res[1];
            }
        }

        return s.substr(res[0], res[1]);
    }
};

滑动窗口

【请复习】滑动窗口的模板

/* 滑动窗口算法框架 */
void slidingWindow(string s) {
    // 用合适的数据结构记录窗口中的数据
    unordered_map<char, int> window;
    
    int left = 0, right = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        window.add(c)
        // 增大窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        // 注意在最终的解法代码中不要 print
        // 因为 IO 操作很耗时，可能导致超时
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (left < right && window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            window.remove(d)
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

Leetcode 3

int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> mp;
    
    int left = 0;
    int right = 0;
    int max_len = 0;
    while (right < s.size()) {
        char c = s[right];
        mp[c]++;
        right++;
        // cout << "left: " << left << " right: " << right << " : ";

        while (mp[c] > 1) {
            char left_c = s[left];
            mp[left_c]--;
            left++;
        } 
        max_len = max(max_len, right-left);
    }
    return max_len;
}

位操作

判断一个 list 中元素出现偶数还是奇数（32 位以内）

vector<int> res = {1, 2, 3, 3, 1}
int result = 0;
for (int i = 0; i < res.size(); ++i) {
    result ^= (1 << res[i]); // 异或操作, 出现一次的位会被设置为1
}

lowbit 操作

快速找到一个数中二进制的最高位置的 1 以及后面所有 0的组合
- 原码 = 101010101000000
- 补码 = 010101011000000
- 原码&补码 = 000000001000000 = 1000000
求二进制中 1 的个数
- 每次都通过 lowbit()获取最高位置的 1 及后续 0 串，然后不断减

#include<iostream>
using namespace std;

int lowbit(int n) {
    return n & (-n);
}

int main() {
    int n, res = 0;
    cin >> n;
    while(n) {
        n -= lowbit(n); //每次减掉最后一个1及其后面所有0的部分
        res++;
    }
    cout << res << endl;
    return 0;
}

判断是否最多只有一个字符出现奇数次的操作，也就是判断一个二进制数字是为全为 0 或仅有一位 1，可配合 lowbit 来做，若 cnt 与 lowbit(cnt) = cnt & -cnt 相等，说明满足要求。
- 考虑到对 lowbit(x) = x & -x 不熟悉的同学，这里再做简单介绍：lowbit(x) 表示 x 的二进制表示最低位的 1 所在的位置对应的值，即仅保留从最低位起的第一个 1，其余位均以 0 填充：
- x = 6，其二进制表示为 110 ，那么 lowbit(6)=(010)=2
- x = 12，其二进制表示为 1100，那么 lowbit(12)=(100)=4

伪回文路径判断条件

mask & (mask - 1) == 0

Leetcode 1457

/**
Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
 */

#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:

    int preTransver(TreeNode* root, int result, int cnt) {
        cout << "check root->val [add one]: " <<  root->val << endl;
        // umap[root->val] += 1;
        cnt ^= (1 << root->val);
        cout << "cnt: " << cnt << endl;
        if (root->left == NULL && root->right == NULL) {
            if (int(cnt & (cnt - 1)) == 0) {
                cout << "is hui wen" << endl;
                
                return result + 1;
            } else {
                cout << "not is hui wen" << endl;
                // umap[root->val] -= 1;
                return result;
            }
        }
        
        if (root->left) {
            result = preTransver(root->left, result, cnt);
            // umap[root->left->val] -= 1;
            // cout << "[sub one]: " << root->left->val << endl;
        }
        
        if (root->right) {
            result = preTransver(root->right, result, cnt);
            // umap[root->right->val] -= 1;
            // cout << "[sub one]: " << root->right->val << endl;
        }
        
        return result;

    }
    int pseudoPalindromicPaths (TreeNode* root) {
        int cnt = 0;
        int result = 0;
        result = preTransver(root, result, cnt);
        return result;
    }
};

int main() {
    TreeNode *root = new TreeNode(2);
    root->left = new TreeNode(1);
    root->right = new TreeNode(1);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(3);
    root->left->right->right = new TreeNode(1);

    Solution *sol = new Solution();

    int result = sol->pseudoPalindromicPaths(root);
    cout << result << endl;
}

C++ 基础

class 中的变量权限

inline

C++ 中的函数调用

CMake

CMake 通常的 build 和编译位置

Ubuntu 安装 CMake

CMakelists 的编写规则

FetchContent 依赖库

CMake 的多版本共存

Makefile

Pybind

C++ 虚函数表

字符串

字符串截取下标段

stoi 和 to_string

数组相关问题

一维数组的排序

前缀和刷题框架

前缀和-vector 实现（1）

前缀和-stack 实现（2）

vector

二维 vector 排序算法

快速创建二维 vector 并初始化为 0

交换 i 和 j 的未知

哈希表

哈希表迭代器

哈希表复杂 key——自定义 Hashfunc 和 Equalfunc

集合

链表

核心思想 qia

反转链表

k 个一组反转链表

二叉树

核心思想

递归解题思路

动态规划 / DFS / 回溯算法

二叉树的深度 后序框架[分解问题框架] + 其他 - Leetcode 543

完美二叉树的三叉树化：可以用于对同层的不同子树进行连接

DFS

BFS (可以用分层 next 链表去替代 queue)

前序遍历 (总是先判断根节点再处理子节点)

后序遍历 (总是先判断两个子节点再处理根节点)

回溯算法

选择-递归-撤销选择的思路

和 DFS 的区别

回溯算法的分类

子集 [元素没有重复、元素不可以重复选]

组合 [元素没有重复、元素不可以重复选]

排列 [元素没有重复、元素不可以重复选]

子集 / 组合 [元素有重复、元素不可以重复选]

排列 [元素有重复、元素不可以重复选]

组合 [元素没有重复、元素可以被重复选]

例子: Leetcode 51 N 皇后

例子: Leetcode 78 返回全排列组合

遍历 for

auto 智能指针

Tuple

C++ 的 deque

C++11 整个专题

lambda

动态规划

Leetcode 1039：切分三角形

Leetcode 2304： 网格中的最小路径代价

BFS

贪心算法

Leetcode 1053 更换顺序字典序最小序列

Leetcode 1042 着色问题

Leetcode 2517 最大最小优化问题

Leetcode 2611 两方离线资源分配问题

单调栈

Leetcode 1019 获取链表的下一个更大的值

【请复习】Leetcode 907 子数组的最小值之和

数论

负二进制模拟

双指针

LCR. 140 链表的倒数第 k 个 node - 快慢指针

Leetcode 1410 字符串匹配和替换

Leetcode 142 环形链表 II

Leetcode 5 最长回文子串

二叉树的深度后序框架[分解问题框架] + 其他 - Leetcode 543

Leetcode 2304：网格中的最小路径代价